Teaching Probability
# Teaching & learning of probability is categorized into 3 philosophical approaches:
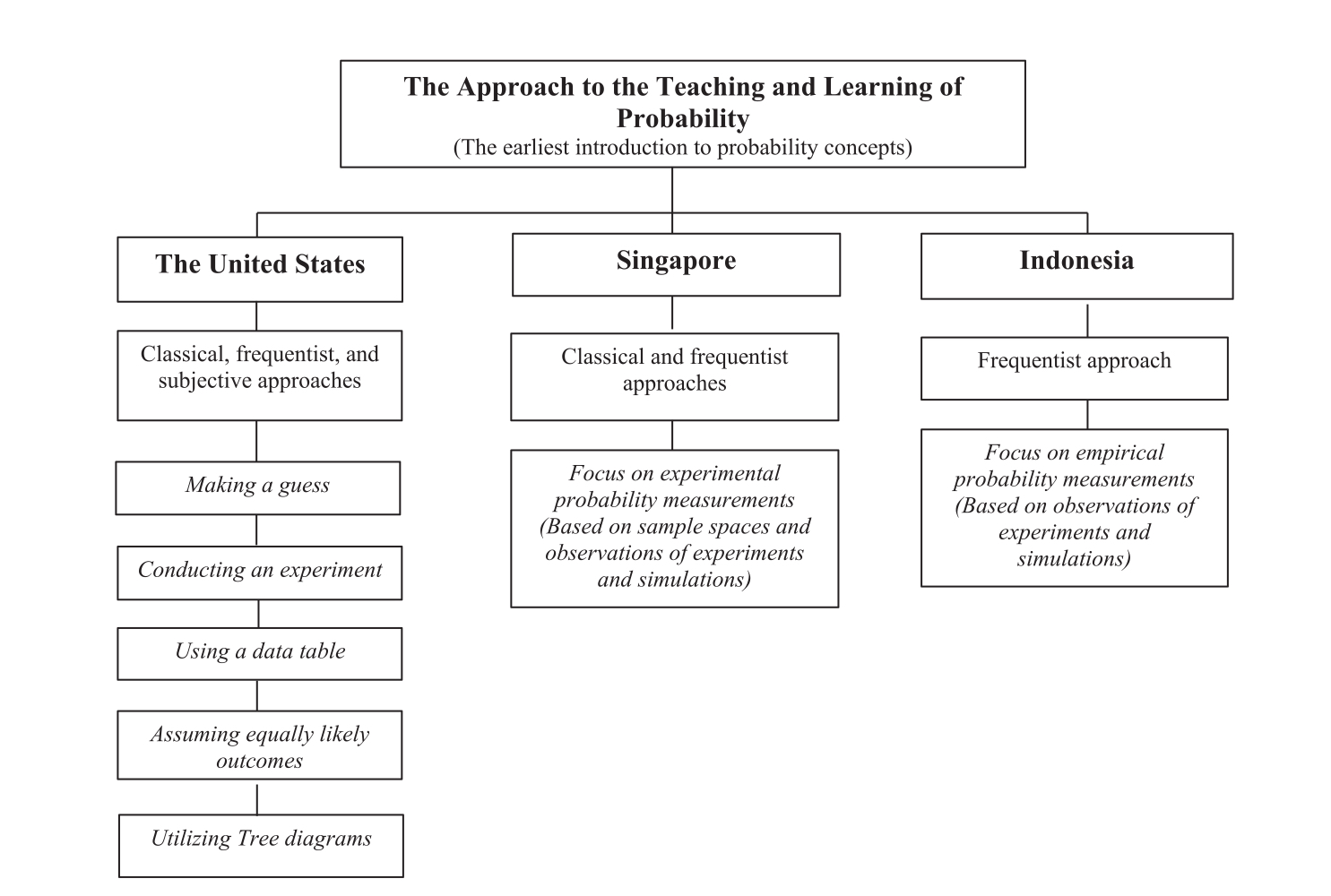
Classical: Formal definition of probabilities in terms of sample spaces of equally likely events, based on a strict set of axioms. Defines probability as a fraction of the number of favorables cases to a particular event divided by the number of all cases possible. Common example: ball being selected from urns
Frequentist: Defines probability of an event as the long-run relative frequency of the event. In other words, the number in which freqency of the event tend towards when an experiment is repeated an infinite number of times. Often taught via simulation.
- Good for confirming intuition, but needs to be complemented with classical approach to understand the ‘why?’
Subjective: Defines probability as a degree of belief, based upon personal judgement and information about an outcome, in which the reptition of the same situation is no longer necessary to give a sense to probability.
- Could be introduced at a more advance level, to help students understand that probabilitic thinking is not fully rational and require subjective input.
# A few ways to distinguish Math textbook:
- Representation forms. Representing math concepts as purely mathematical, written, visual or combined forms.
- Cogntive demand levels. What level of cognitive demand does textbook question afford? Low cognitive demand - memorization, procedures without connection. High cognitive demand - Procedure with connection, open-ended math problem.
- Contextual features. How relevant is problem context to student’s everyday life?
# Synthesising
Why teach probability?
- Framework for thinking and sound decision making.
Logical understanding on how probability works is indispensable to the key to the transferability of probabilitistic concepts to real life scenarios. This can best be achieved by setting questions with high cognitive demand, in addition to providing high contextualized examples.
Indonesian textbook sets questions that are high contextualized, but requires low cognitive demand. Their students report low performance on context-based mathemtics tasks; Only 1% of their students could work with context-based problems in complex situations. This is because they do not fundamentally understand the concepts of probability. Completing taks that requires higher congitive demand levels can faciliate a productive struggle which helps them make missing connections.